MATHS :: Lecture 05 :: Differential Calculus(1)

DIFFERENTIATION

In all practical situations we come across a number of variables. The variable is one which takes different values, whereas a constant takes a fixed value.
Let x be the independent variable. That means x can take any value. Let y be a variable depending on the value of x. Then y is called the dependent variable. Then y is said to be a function of x and it is denoted by y = f(x)
For example if x denotes the time and y denotes the plant growth, then we know that the plant growth depends upon time. In that case, the function y=f(x) represents the growth function. The rate of change of y with respect to x is denoted by and called as the derivative of function y with respect to x.

S.No.

Form of Functions

y=f(x)

1.

Power Formula

xn

2.

Constant

C

0

3.

Constant with variable

Cy

4.

Exponential

ex                   

ex

5.

Constant power x

ax

    ax log a

6.

Logirthamic

logx                

7.

Differentiation of a sum

y = u + v
where u and v are functions of x. 

8.

Differentiation of  a difference

y = u – v
where u and v are functions of x. 

9.

Product rule of differentiation

y = uv,
where u and v are functions of x. 

10.

Quotient rule of differentiation

 y =  ,
where u and v are functions of x. 


where    ,

Example

  1. Differentiate each of the following function   

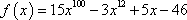
Solution

  1. Differentiate following function   

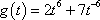
Solution
  Here is the derivative.

  1. Differentiate following function   

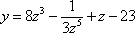
Solution

diff. w.r.to  x

MPSetEqnAttrs('eq0008','',3,[[90,34,13,-1,-1],[118,46,17,-1,-1],[148,57,21,-1,-1],[],[],[],[372,141,53,-3,-3]]);  
ExampleBegin(); 4.  Differentiate  the following functions.
a)                                                                                                                             
Solution
MPSetEqnAttrs('eq0009','',3,[[84,18,5,-1,-1],[111,24,7,-1,-1],[139,31,8,-1,-1],[],[],[],[348,77,21,-3,-3]]) MPEquation()                              
MPSetEqnAttrs('eq0011','',3,[[76,23,5,-1,-1],[101,32,7,-1,-1],[127,40,8,-1,-1],[],[],[],[315,98,22,-3,-3]]) MPEquation()
diff   y  w.  r. to  x    MPSetEqnAttrs('eq0012','',3,[[154,27,9,-1,-1],[205,38,13,-1,-1],[257,47,16,-1,-1],[],[],[],[641,114,39,-3,-3]]) MPEquation()
MPSetEqnAttrs('eq0012','',3,[[154,27,9,-1,-1],[205,38,13,-1,-1],[257,47,16,-1,-1],[],[],[],[641,114,39,-3,-3]]);   MPSetEqnAttrs('eq0013','',3,[[132,62,28,-1,-1],[175,83,37,-1,-1],[218,105,47,-1,-1],[],[],[],[547,258,117,-3,-3]]);   
ExampleBegin(); 5. Differentiate  the following functions.   MPSetEqnAttrs('eq0014','',3,[[218,34,14,-1,-1],[289,45,19,-1,-1],[361,55,23,-1,-1],[],[],[],[905,141,58,-3,-3]]) MPEquation() MPSetEqnAttrs('eq0009','',3,[[84,18,5,-1,-1],[111,24,7,-1,-1],[139,31,8,-1,-1],[],[],[],[348,77,21,-3,-3]]);

MPSetEqnAttrs('eq0010','',3,[[130,17,6,-1,-1],[172,22,7,-1,-1],[216,27,8,-1,-1],[],[],[],[539,71,22,-3,-3]]) MPEquation()
diff  f(x)  w r to x
                                                  

Derivatives of the six trigonometric  functions
 

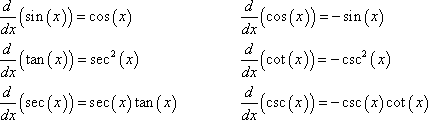
Example
1.  Differentiate each of the following functions.
 
Solution   We’ll just differentiate each term using the  formulas from above.

2.  Differentiate each of the following functions
Here’s the derivative of this function.

 Note that in the simplification step we took advantage of the fact that

to simplify the second term a little.
3.  Differentiate each of the following functions
  In this part we’ll need to use the quotient rule.

 

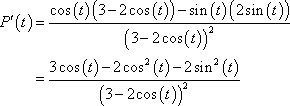
Download this lecture as PDF here