MATHS :: Lecture 10 :: INTEGRATION

INTEGRATION
Integration is a process, which is a inverse of differentiation. As the symbol  represents differentiation with respect to x, the symbol  stands for integration with respect to x.
Definition
If  then f(x) is called the integral of F(x) denoted by . This can be read it as integral of F(x) with respect to x is f(x) + c where c is an arbitrary constant. The integral  is known as Indefinite integral and the function F(x) as integrand.

Integration by parts Examples I

Integration by parts Examples II

Integration by parts Examples III

      Formula on integration
1).  +c  ( n ¹-1)
2). +c 
3). =  x+c 
4). +c 
5). dx = ex +c 
6).  
7). 
 8).  = c x + d
 9). +c 
10). +c 
11). +c 
12). +c 
13).
14).
13). 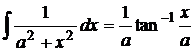+c 
14). +c 

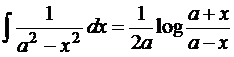15). +c 
16).

Definite integral
If  f(x)  is indefinite integral of F(x) with respect to x then the Integral  is called definite integral of F(x) with respect to x from x = a to x = b. Here a is called the Lower limit and b is called the Upper limit of the integral.
  =     =  f(Upper limit ) - f(Lower limit)
=  f(b) - f(a)
Note
While evaluating a definite integral no constant of integration is to be added. That is a definite integral has a definite value.

Method of substitution

Method –1
Formulae for the functions involving (ax + b)
Consider the integral
I = -------------(1)
Where a and b are constants
Put a x + b = y
Differentiating with respect to x
a dx + 0 = dy

Substituting in (1)
I = +c
=+c
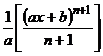=+c
=+ c
Similarly this method can be applied for other formulae also.

Method II
Integrals of the functions of the form

put =y,


Substituting we get
I = and this can be integrated.
Method –III
Integrals of function of the type
when n ¹ -1, put f(x) = y then
\ =
                                  =
                                 = 
when n= -1, the integral reduces to

putting y = f(x) then dy = f1(x) dx
\=log f(x)
Method IV

Method of Partial Fractions

Integrals of the form
Case.1
If denominator can be factorized into linear factors then we write the integrand as
the sum or difference of  two linear factors of the form

Case-2

In the given   integral     the denominator ax2 + bx + c can not be factorized into linear factors, then express ax2 + bx + c as the sum or difference of two perfect squares and then apply the formulae

Integrals of the form
Write denominator as the sum or difference of two perfect squares
=  or   or 
and then apply the formula
 = log(x+
 = log(x+
 = 
Integration by parts
If the given integral is of the form   then this can not be solved by any of techniques studied so  far. To solve this  integral we first take the product rule on differentiation
=u +v
Integrating both sides we get
dx= ( u +v )dx
then we have    u v=+
re arranging the terms we   get
 = uv-   This formula is known as integration by parts formula
Select the functions u and dv appropriately in such a way that integral can be more easily integrable than the given integral

 

Application of integration
The area bounded by the function y=f(x), x=axis and the ordinates at x=a x=b is given by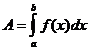

 

Download this lecture as PDF here