MATHS:: Lecture 15 :: Partial Differentiation
![]()
Chain Rule differentiation
If y is a function of u ie y = f(u) and u is a function of x ie u = g(x) then y is related to x through the intermediate function u ie y =f(g(x) )
\y is differentiable with respect to x
Furthermore, let y=f(g(x)) and u=g(x), then
![]() =
=![]()
![]()
There are a number of related results that also go under the name of "chain rules." For example, if y=f(u) u=g(v), and v=h(x),
then ![]() =
= ![]()
Problem
Differentiate the following with respect to x
- y = (3x2+4)3
- y =
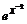
Marginal Analysis
Let us assume that the total cost C is represented as a function total output q. (i.e) C= f(q).
Then marginal cost is denoted by MC=![]()
The average cost = ![]()
Similarly if U = u(x) is the utility function of the commodity x then
the marginal utility MU = ![]()
The total revenue function TR is the product of quantity demanded Q and the price P per unit of that commodity then TR = Q.P = f(Q)
Then the marginal revenue denoted by MR is given by ![]()
The average revenue = ![]()
Problem
1. If the total cost function is C = Q3 - 3Q2 + 15Q. Find Marginal cost and average cost.
Solution:
MC = ![]()
AC = ![]()
2. The demand function for a commodity is P= (a - bQ). Find marginal revenue.
(the demand function is generally known as Average revenue function). Total revenue TR = P.Q = Q. (a - bQ) and marginal revenue MR= ![]()
Growth rate and relative growth rate
The growth of the plant is usually measured in terms of dry mater production and as denoted by W. Growth is a function of time t and is denoted by W=g(t) it is called a growth function. Here t is the independent variable and w is the dependent variable.
The derivative ![]() is the growth rate (or) the absolute growth rate gr=
is the growth rate (or) the absolute growth rate gr=![]() . GR =
. GR = ![]()
The relative growth rate i.e defined as the absolute growth rate divided by the total
dry matter production and is denoted by RGR.
i.e RGR = ![]() .
. ![]() =
= ![]()
Problem
- If G = at2+b sin t +5 is the growth function function the growth rate and relative growth rate.
GR = ![]()
RGR = ![]() .
. ![]()
Implicit Functions
If the variables x and y are related with each other such that f (x, y) = 0 then it is called Implicit function. A function is said to be explicit when one variable can be expressed completely in terms of the other variable.
For example, y = x3 + 2x2 + 3x + 1 is an Explicit function
xy2 + 2y +x = 0 is an implicit function
Problem
For example, the implicit equation xy=1 can be solved by differentiating implicitly gives
![]() =
=![]()
![]()
![]()
Implicit differentiation is especially useful when y’(x)is needed, but it is difficult or inconvenient to solve for y in terms of x.
Example: Differentiate the following function with respect to x ![]()
![]()
Solution
So, just differentiate as normal and tack on an appropriate derivative at each step. Note as well that the first term will be a product rule.
![]()
![]()
![]()
![]()
Example: Find ![]()
![]()
![]()
![]()
![]() for the following function.
for the following function.
![]()
![]()
![]()
![]()
Solution
In this example we really are going to need to do implicit differentiation of x and write y as y(x).
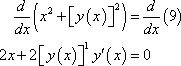
![]()
![]()
![]()
Notice that when we differentiated the y term we used the chain rule.
Example:
Find ![]()
![]()
![]()
![]()
![]() for the following.
for the following. ![]()
![]()
![]()
![]()
Solutio
First differentiate both sides with respect to x and notice that the first time on left side will be a product rule.
![]()
![]()
![]()
![]()
Remember that very time we differentiate a y we also multiply that term by ![]()
![]()
![]()
![]()
![]()
![]() since we are just using the chain rule. Now solve for the derivative.
since we are just using the chain rule. Now solve for the derivative.
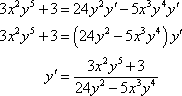
![]()
![]()
![]()
The algebra in these can be quite messy so be careful with that.
Example
Find ![]()
![]()
![]()
![]()
![]() for the following
for the following ![]()
![]()
![]()
![]()
Here we’ve got two product rules to deal with this time.
![]()
![]()
![]()
![]()
Notice the derivative tacked onto the secant. We differentiated a y to get to that point and so we needed to tack a derivative on.
Now, solve for the derivative.
![]()
![]()
![]()
Logarithmic Differentiation
For some problems, first by taking logarithms and then differentiating,
it is easier to find ![]() . Such process is called Logarithmic differentiation.
. Such process is called Logarithmic differentiation.
- If the function appears as a product of many simple functions then by
taking logarithm so that the product is converted into a sum. It is now
easier to differentiate them.
- If the variable x occurs in the exponent then by taking logarithm it is
reduced to a familiar form to differentiate.
ExampleBegin(); Example Differentiate the function.
MPSetEqnAttrs('eq0001','',3,[[100,34,16,-1,-1],[133,45,21,-1,-1],[166,56,26,-1,-1],[],[],[],[415,139,67,-3,-3]]) MPEquation() ![]()
![]()
![]()
![]()
MPSetEqnAttrs('eq0001','',3,[[100,34,16,-1,-1],[133,45,21,-1,-1],[166,56,26,-1,-1],[],[],[],[415,139,67,-3,-3]]); SolutionDifferentiating this function could be done with a product rule and a quotient rule. We can simplify things somewhat by taking logarithms of both sides.
MPSetEqnAttrs('eq0002','',3,[[134,40,17,-1,-1],[177,53,22,-1,-1],[221,67,29,-1,-1],[],[],[],[554,165,70,-3,-3]]) MPEquation() 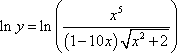
![]()
![]()
![]()
MPSetEqnAttrs('eq0002','',3,[[134,40,17,-1,-1],[177,53,22,-1,-1],[221,67,29,-1,-1],[],[],[],[554,165,70,-3,-3]]); MPSetEqnAttrs('eq0003','',3,[[190,49,22,-1,-1],[253,67,30,-1,-1],[316,84,37,-1,-1],[],[],[],[792,215,95,-3,-3]]) MPEquation() 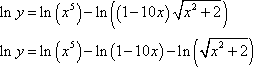
![]()
![]()
![]()
MPSetEqnAttrs('eq0003','',3,[[190,49,22,-1,-1],[253,67,30,-1,-1],[316,84,37,-1,-1],[],[],[],[792,215,95,-3,-3]]); MPSetEqnAttrs('eq0004','',3,[[175,89,42,-1,-1],[233,118,55,-1,-1],[291,148,69,-1,-1],[],[],[],[729,368,173,-3,-3]]) MPEquation() 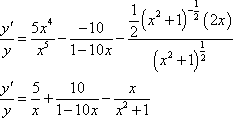
![]()
![]()
![]()
ExampleBegin(); Example Differentiate MPSetEqnAttrs('eq0007','',3,[[30,11,3,-1,-1],[39,15,3,-1,-1],[47,17,3,-1,-1],[],[],[],[119,44,9,-3,-3]]) MPEquation() ![]()
![]()
![]()
![]()
![]()
MPSetEqnAttrs('eq0007','',3,[[30,11,3,-1,-1],[39,15,3,-1,-1],[47,17,3,-1,-1],[],[],[],[119,44,9,-3,-3]]); Solution
First take the logarithm of both sides as we did in the first example and use the logarithm properties to simplify things a little.
MPSetEqnAttrs('eq0009','',3,[[54,30,13,-1,-1],[73,39,16,-1,-1],[90,48,20,-1,-1],[],[],[],[227,120,52,-3,-3]]) MPEquation() ![]()
![]()
![]()
MPSetEqnAttrs('eq0009','',3,[[54,30,13,-1,-1],[73,39,16,-1,-1],[90,48,20,-1,-1],[],[],[],[227,120,52,-3,-3]]); Differentiate both sides using implicit differentiation.
MPSetEqnAttrs('eq0010','',3,[[121,30,12,-1,-1],[162,39,16,-1,-1],[203,49,20,-1,-1],[],[],[],[507,124,50,-3,-3]]) MPEquation() ![]()
![]()
![]()
![]()
MPSetEqnAttrs('eq0010','',3,[[121,30,12,-1,-1],[162,39,16,-1,-1],[203,49,20,-1,-1],[],[],[],[507,124,50,-3,-3]]); As with the first example multiply by y and substitute back in for y.
MPSetEqnAttrs('eq0011','',3,[[75,34,14,-1,-1],[99,45,19,-1,-1],[123,57,23,-1,-1],[],[],[],[310,145,61,-3,-3]]) MPEquation() ![]()
![]()
![]()
![]()
PARAMETRIC FUNCTIONS
Sometimes variables x and y are expressed in terms of a third variable called parameter. We find ![]() without eliminating the third variable.
without eliminating the third variable.
Let x = f(t) and y = g(t) then
![]() =
= ![]()
= 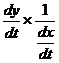 =
= ![]()
Problem
1. Find for the parametric function x =a cos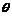 , y = b sin
, y = b sin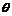
Solution
![]()
![]()
![]() =
= ![]()
=![]()
=![]()
Inference of the differentiation
Let y = f(x) be a given function then the first order derivative is ![]() .
.
The geometrical meaning of the first order derivative is that it represents the slope of the curve y = f(x) at x.
The physical meaning of the first order derivative is that it represents the rate of change of y with respect to x.
PROBLEMS ON HIGHER ORDER DIFFERENTIATION
The rate of change of y with respect x is denoted by ![]() and called as the first order derivative of function y with respect to x.
and called as the first order derivative of function y with respect to x.
The first order derivative of y with respect to x is again a function of x, which again be differentiated with respect to x and it is called second order derivative of y = f(x) and is denoted by ![]() which is equal to
which is equal to ![]()
In the similar way higher order differentiation can be defined. Ie. The nth order derivative of y=f(x) can be obtained by differentiating n-1th derivative of y=f(x)
![]() where n= 2,3,4,5….
where n= 2,3,4,5….
Problem
Find the first , second and third derivative of
- y =
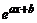
- y = log(a-bx)
- y = sin (ax+b)
Partial Differentiation
So far we considered the function of a single variable y = f(x) where x is the only independent variable. When the number of independent variable exceeds one then we call it as the function of several variables.
Example
z = f(x,y) is the function of two variables x and y , where x and y are independent variables.
U=f(x,y,z) is the function of three variables x,y and z , where x, y and z are independent variables.
In all these functions there will be only one dependent variable.
Consider a function z = f(x,y). The partial derivative of z with respect to x denoted by ![]() and is obtained by differentiating z with respect to x keeping y as a constant. Similarly the partial derivative of z with respect to y denoted by
and is obtained by differentiating z with respect to x keeping y as a constant. Similarly the partial derivative of z with respect to y denoted by ![]() and is obtained by differentiating z with respect to y keeping x as a constant.
and is obtained by differentiating z with respect to y keeping x as a constant.
Problem
1. Differentiate U = log (ax+by+cz) partially with respect to x, y & z
We can also find higher order partial derivatives for the function z = f(x,y) as follows
(i) The second order partial derivative of z with respect to x denoted as ![]() is obtained by partially differentiating
is obtained by partially differentiating ![]() with respect to x. this is also known as direct second order partial derivative of z with respect to x.
with respect to x. this is also known as direct second order partial derivative of z with respect to x.
(ii)The second order partial derivative of z with respect to y denoted as ![]() is obtained by partially differentiating
is obtained by partially differentiating ![]() with respect to y this is also known as direct second order partial derivative of z with respect to y
with respect to y this is also known as direct second order partial derivative of z with respect to y
(iii) The second order partial derivative of z with respect to x and then y denoted as ![]() is obtained by partially differentiating
is obtained by partially differentiating ![]() with respect to y. this is also known as mixed second order partial derivative of z with respect to x and then y
with respect to y. this is also known as mixed second order partial derivative of z with respect to x and then y
iv) The second order partial derivative of z with respect to y and then x denoted as
![]() is obtained by partially differentiating
is obtained by partially differentiating ![]() with respect to x. this is also known as mixed second order partial derivative of z with respect to y and then x.
with respect to x. this is also known as mixed second order partial derivative of z with respect to y and then x.
In similar way higher order partial derivatives can be found.
Problem
Find all possible first and second order partial derivatives of
1) z = sin(ax +by)
2) u = xy + yz + zx
Homogeneous Function
A function in which each term has the same degree is called a homogeneous function.
Example
- x2 - 2xy + y2 = 0 ® homogeneous function of degree 2.
- 3x +4y = 0 ® homogeneous function of degree 1.
- x3 +3x2y + xy2 – y3= 0 ® homogeneous function of degree 3.
To find the degree of a homogeneous function we proceed as follows.
Consider the function f(x,y) replace x by tx and y by ty if f (tx, ty) = tn f(x, y) then n gives the degree of the homogeneous function. This result can be extended to any number of variables.
Problem
Find the degree of the homogeneous function
- f(x, y) = x2 –2xy + y2
- f(x,y) =
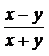
Euler’s theorem on homogeneous function
If U= f(x,y,z) is a homogeneous function of degree n in the variables x, y & z then ![]()
![]()
Problem
Verify Euler’s theorem for the following function
1. u(x,y) = x2 –2xy + y2
2. u(x,y) = x3 + y3+ z3–3xyz
Increasing and decreasing function
Increasing function
A function y= f(x) is said to be an increasing function if f(x1) < f(x2) for all x1 < x2.
The condition for the function to be increasing is that its first order derivative is always
greater than zero .
i.e ![]() >0
>0
Decreasing function
A function y= f(x) is said to be a decreasing function if f(x1) > f(x2) for all x1 < x2.
The condition for the function to be decreasing is that its first order derivative is always
less than zero .
i.e ![]() < 0
< 0
Problems
1. Show that the function y = x3 + x is increasing for all x.
2. Find for what values of x is the function y = 8 + 2x – x2 is increasing or decreasing ?
Maxima and Minima Function of a single variable
A function y = f(x) is said to have maximum at x = a if f(a) > f(x) in the neighborhood of the point x = a and f(a) is the maximum value of f(x) . The point x = a is also known as local maximum point.
A function y = f(x) is said to have minimum at x = a if f(a) < f(x) in the neighborhood of the point x = a and f(a) is the minimum value of f(x) . The point x = a is also known as local minimum point.
The points at which the function attains maximum or minimum are called the turning points or stationary points
A function y=f(x) can have more than one maximum or minimum point.
Maximum of all the maximum points is called Global maximum and minimum of all the minimum points is called Global minimum.
A point at which neither maximum nor minimum is called Saddle point.
[Consider a function y = f(x). If the function increases upto a particular point x = a and then decreases it is said to have a maximum at x = a. If the function decreases upto a point x = b and then increases it is said to have a minimum at a point x=b.]
The necessary and the sufficient condition for the function y=f(x) to have a maximum or minimum can be tabulated as follows
|
Maximum |
Minimum |
First order or necessary condition |
|
|
Second order or sufficient condition |
|
|
Working Procedure
1. Find 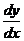 and
and 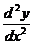
2. Equate 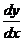 =0 and solve for x. this will give the turning points of the function.
=0 and solve for x. this will give the turning points of the function.
3. Consider a turning point x = a then substitute this value of x in 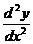 and find the
and find the
nature of the second derivative. If 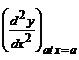 < 0, then the function has a maximum
< 0, then the function has a maximum
value at the point x = a. If 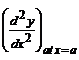 > 0, then the function has a minimum value at
> 0, then the function has a minimum value at
the point x = a.
4. Then substitute x = a in the function y = f(x) that will give the maximum or minimum
value of the function at x = a.
Problem
Find the maximum and minimum values of the following function
y = x3 – 3x +1
| Download this lecture as PDF here |
![]()