MATHS :: Lecture 11 :: INVERSE OF A MATRIX

 
INVERSE OF A MATRIX
Definition
Let A be any square matrix.  If there exists another square matrix B Such that AB = BA = I (I is a unit matrix) then B is called the inverse of the matrix A and is denoted by A-1.
The cofactor method is used to find the inverse of a matrix. Using matrices, the solutions of simultaneous equations are found.                                                     
Working Rule to find the inverse of the matrix
Step 1: Find the determinant of the matrix.
Step 2: If the value of the determinant is non zero proceed to find the inverse of the matrix.
Step 3: Find the cofactor of each element and form the cofactor matrix.
Step 4: The transpose of the cofactor matrix is the adjoint matrix.
Step 5:  The inverse of the matrix A-1 =


Finding Matrix Inverse

Inverse Matrices

Cramer's Rule, Inverse Matrix, and Volume

Example
Find the inverse of the matrix
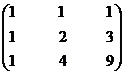
Solution
Let A =
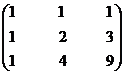
Step 1

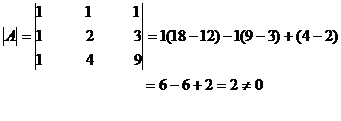
Step 2
The value of the determinant is non zero
\A-1 exists.
Step 3
Let Aij denote the cofactor of aij in









Step 4
The matrix formed by cofactors of element of determinant  is
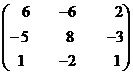
\adj A =
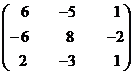
Step 5

=
                 
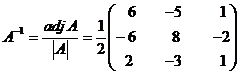
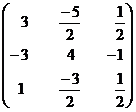
SOLUTION OF LINEAR EQUATIONS
Let us consider a system of linear equations with three unknowns

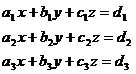
The matrix form of the equation is AX=B where 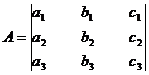is a 3x3 matrix
X =  and B =
Here AX = B
Pre multiplying both sides by A‑1.
(A-1 A)X= A-1B
We know that A-1 A= A A-1=I
\ I X= A-1B
since IX = X
Hence the solution is X =  A-1B.
Example
Solve the x + y + z = 1, 3x + 5y + 6z = 4, 9x + 26y + 36z =16 by matrix method.
Solution
The given equations are    x + y + z = 1,
3x + 5y + 6z = 4,
9x + 26y + 36z =16

Let A= 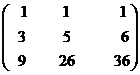, X=, B=
The given system of equations can be put in the form of the matrix equation AX=B

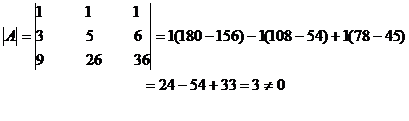
The value of the determinant is non zero
\ A-1 exists.
Let Aij (i, j = 1,2,3) denote the cofactor of aij in









The matrix formed by cofactors of element of determinant  is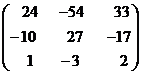
\adj A =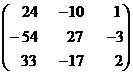


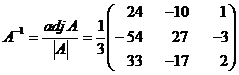
We Know that      X=A-1B

\  =           
 
=
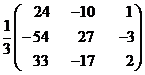
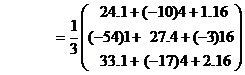
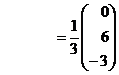x = 0, y = 2, z = -1.
SOLUTION BY DETERMINANT (CRAMER'S RULE)
Let the equations be
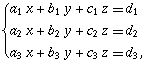{a_1x+b_1y+c_1z==d_1; a_2x+b_2y+c_2z==d_2; a_3x+b_3y+c_3z==d_3,        …………………….  (1)            
Consider the determinant

                            
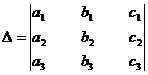
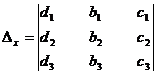
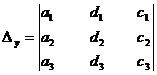
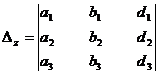
When D ≠ 0, the unique solution is given by
              
Example
Solve the equations x + 2y + 5z =23, 3x + y + 4z = 26,                           6x + y + 7z = 47 by determinant method (Cramer’s Rule).
Solution
The equations are
x + 2y + 5z =23,
3x + y + 4z = 26,
6x + y + 7z = 47
      
         
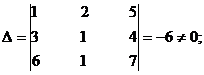
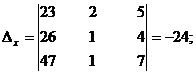
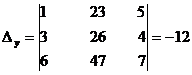
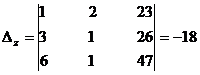
By Cramer’s rule

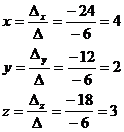
Þ x = 4, y = 2, z = 3.

 

Download this lecture as PDF here